Most people should already be aware of the KM functions which generate random numbers:
RAND(A) returns a random integer from ZERO to A-1
RAND(A,B) returns a random integer from A to B (could even return B)
RANDOM(A) returns a random real number from ZERO to A
RANDOM(A,B) returns a random real number from A to B
Here's the official wiki page about it....
https://wiki.keyboardmaestro.com/function/RAND
But I would like to take this one small step further... for those people who need to mimic random values found in nature.
In all of the examples above, each possible number that could be returned is "equally likely." For most people, this is good enough for their purposes. But sometimes I need some numbers to be more likely than others.
For example, as a human being, when I pause to look at the screen and read a message, it may take me an average of 10 seconds to read the message. Sometimes I could read it in 9 or 11 seconds, and sometimes I could read it in 8 or 12 seconds, but each additional second away from 10 it would be less likely that I would read it in that amount of time. So if I was trying to write a macro that mimicked a human's pause, it would need to be more "skewed" like this. I wouldn't be able to simply say "PAUSE for RAND(5,15) seconds" to mimic a human's behaviour because all the values returned by that function, in the range of 5 to 15, are equally likely, and that's not how humans behave. In order to make a PAUSE statement that paused for some number of seconds around 10 seconds, but with no lower or upper limit, it could look like this:
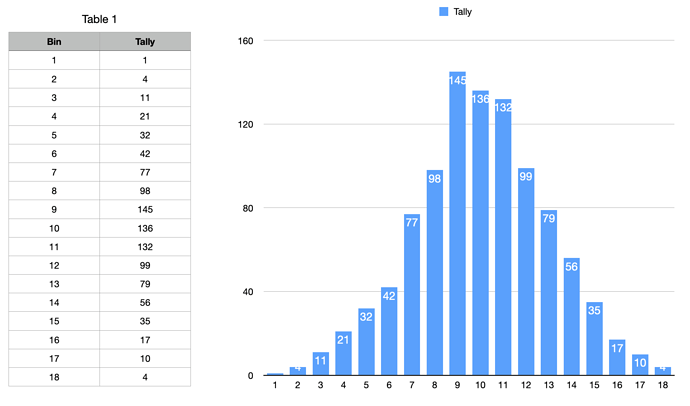
There is some advanced mathematical witchcraft in there which I won't explain, other than the opening "10 + 3 * " which brings the average result returned to be about 10. I ran that statement in a loop 1000 times, and I stored the results in "bins" (using a dictionary) and here's the result I got:
NOTE: In my example above, the "10 +" simply moves the curve upwards to the value 10, and "3 * " flattens the curve a bit. Nothing magical there.
If you look at the chart, the number 9 actually came up more than 10 during this run of 1000 occurrences. That's fine, and not unexpected, because small samples can return deviations from the norm. In fact, this curve is called the Normal Distribution Curve. Every measurement in nature fits this distribution, from the heights of all people, to the weights of all elephants, to the length of time that people require to read a sentence. This is what true "random natural samples" look like. But most languages don't support random numbers that match this form of natural number distribution. That's why I had to use an advanced formula above to simulate it. There are a few other formulas that can also do the job, but this one seems the simplest to use in KM.
Here it is for you to copy and paste: (this curve is centred around the number zero, so you may need to do what I did above to centre it around your preferred value.)
COS(2*3.1415926*RANDOM(0,1))*SQRT(-2*LOG(RANDOM(0,1)))
A common requirement is to take the ABSOLUTE VALUE of this expression (using KM's "ABS()" function) if you want the "most common number returned" to be near zero, with positive numbers becoming less likely.
Another term used in mathematics to describe this process is the "Probability Density Function", abbreviated as "PDF." The built-in KM RANDOM functions have a flat PDF, while the PDF for the function I provided above has a PDF in the shape of a Normal Distribution Curve. This is what you need to generate random numbers that mimic natural measurements.
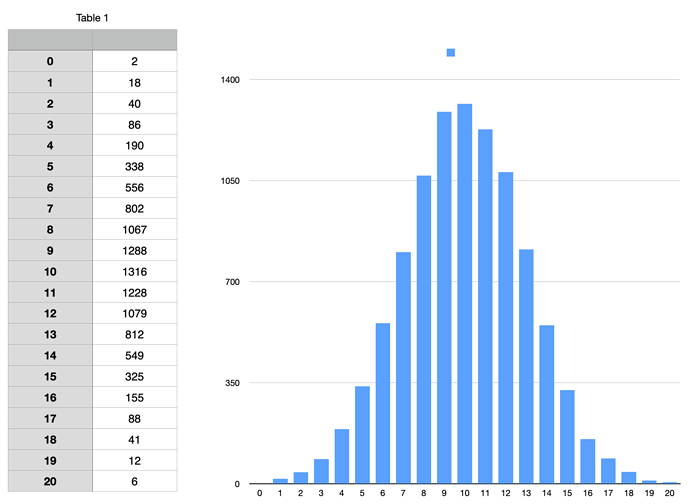
Here's what the curve looked like after 9,998 samples: (the chart looks smoother due to the larger sample size)
I've been using this formula for about 10 years to simulate natural things like human behaviour.
For those who are interested, here's the code I used today to create these tallies. It uses a dictionary to save its values.
Normal Distribution PDF Macro (v10.0.2)
Normal Distribution PDF.kmmacros (9.0 KB)