My inputs look like this:
19 Jan. 2024
I want to find out the number of days (or time elapsed, roughly) since then.
I can do it with Wolfram Alpha
So, the answer is roughly 41 days
All date formats are like this:
in other words, the month is shortened with a dot at the end.
Hang on, i just found this Calculate days between two dates
But i don't know how to convert the date format into 10/05/18
Oh and it's also confusing because here in the UK we use day/month/year not month/day/year 
I could use the JD function (Julian Date) to convert 19 Jan. 2024.
So would that be JD(19 Jan. 2024)?
Oh shoot I can't do that because it has to be in this format:
JD( year, month, day )
so it would need to be JD(2024, 01, 19) presumably
Hmm. I suppose I could use RegEx to do this
update -- today is simply JD()
So that gives the right answer! That is super encouraging!
Some elements summarised here may be relevant:
If the format is always dd Mmm yyyy, then the regex should just be:
^(\d{2}) (.*?) (\d{4})
But you'd then have to take one more step to convert Jan to 1, Feb to 2, etc.
-rob.
i came up with
^(\d{1,2}) (\w{3,}?.?) (\d{4})
since the day can be 1 or 2 digits (e.g. 1 or 20)
But i'm not quite sure how to do the capture groups correctly
(and yes, I then need to convert Jan to 1 and Feb to 2 etc.)
Using something like this maybe:
And can I do it more elegantly (using subroutines?) Or is it best to just copy paste it 12 times ?
Should work. If the day of the month can be one or two digits, you could use \d+ instead of the {1,2}.
You can make it simpler with a multi-line variable and a bit of shell command magic:
Download Macro(s): Convert month to number.kmmacros (5.8 KB)
-rob.
If i want to reuse this code for future variables (perhaps Month2 and Month3) then can I make this into a subroutine?
Or I could just duplicate the Macro and edit the variable
If you do this a lot, I'd probably make the list of months a global variable. Then you could make a subroutine that takes the month name as input, and just runs the Terminal command (but referencing the global variable) and returns the month number.
-rob.
oh you can set a variable to multiple strings separated by a return? I didn't know that!
I note that case sensitivity matters.
can I make it so that
Jan = Jan. = jan. = jan = January
Thanks!
EDIT: i must try to teach myself grep/ shell scripts
The demo macro I attached shows the variable as a multi-line entry. That's the key to how it works: The shell commands simply shows (echo) that variable, then sends that output to grep to search fore the month name, but with a flag (-n) that also returns the line number where the match was found. The last bit, the cut command, trims everything but the line number.
If you have multiple variations on the month name, you could just list them all on the same line of the variable:
etc
Aug August Aug. august aug.
Sep September Sep. September sep.
etc
The grep command will then still find the occurrence on the proper line. Note that this is a very simple grep, and as such, if you entered a month of Au, it would find it, because August contains Au. There are ways of doing more exact matching, but it shouldn't be required given you have control over the naming.
-rob.
Hi, friends. I'm not back to this forum permanently because I'm enjoying a relaxing long break but I do read a few posts now and then, and this request really intrigued me:
Perhaps I've got OCD when it comes to finding and writing "one line solutions" for problems like this. I decided to tackle this one. My solution is not desirable for the average person, it's simply an academic exercise at writing concise code. At the bottom of this post is my one-line solution for converting a date like this:
12 SEP. 2025
to a set of numbers like this:
12 9 2025
Notice that I chose to use capital letters for the date instead of lowercase, which was just accidental. I could also come up with a solution for mixed-case month names, if anyone wants to see that.
Understanding how my solution works is tough enough for anyone reading this, but figuring out how I came up with the numeric values in the solution is much tougher. There are millions of possible choices for the numeric values, and I just randomly picked the first one I saw.
Here is my solution: (In this example I'm using a text box for input to a shell script, which is the simplest way I could think of to create an example. I suppose you could use KM Variables if you wanted to.)
Here is the text in an easier-to-copy format...
sed "s/ /;((0/" | tr ' ' ';' | sed "s/[ABCDLMO]//g;s/E/+11/;s/F/+2/;s/G/+2/;s/J/+1/;s/N/+11/;s/P/+1/;s/R/+2/;s/S/+8/;s/T/+9/;s/U/+5/;s/V/+11/;s/Y/4/;s/./)%12)+1/" | bc | tr '\n' ' '
If anyone actually tries to figure out how this works, I would be happy to give some clues if you get stuck. But I'd like to wait a week before I drop clues, in case anyone wants to try to figure it out. I think it would be a very rewarding puzzle to try to solve. I didn't time myself, but it took a couple of hours to develop the methods I needed to solve this.
I would be convinced that you understand this code if you come up with an identical piece of code but you replace ABCDLMO with a different set of letters. My approach is so esoteric I can safely predict that nobody on the Internet has a similar approach.
you are a scholar and a gentleman
Do you have KM11 or KM10?
-rob.
If you are running a pre-11 version of Keyboard Maestro, you could just remove ‘return’ from the start of the Javascript expression
(but you would benefit more from an upgrade 
)
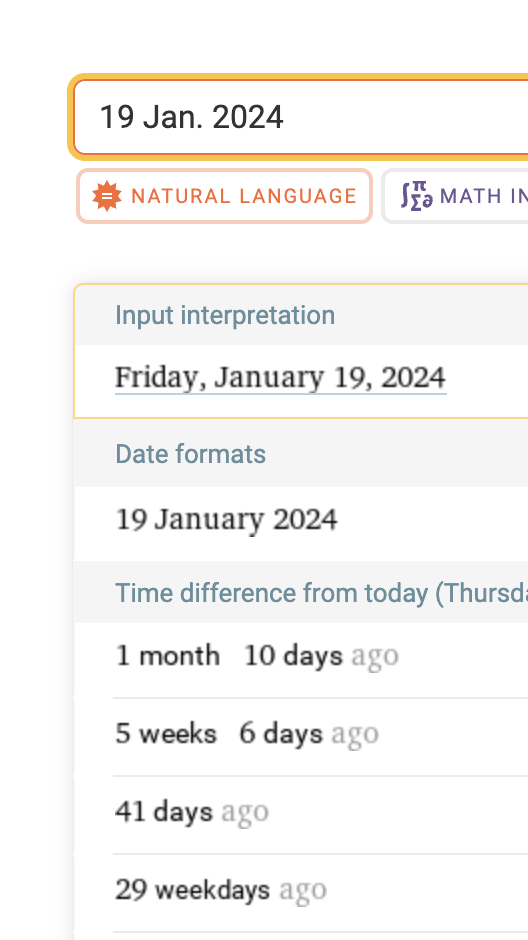
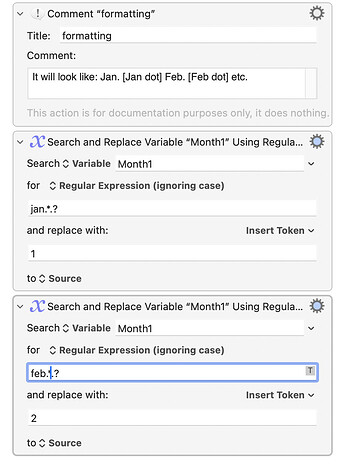
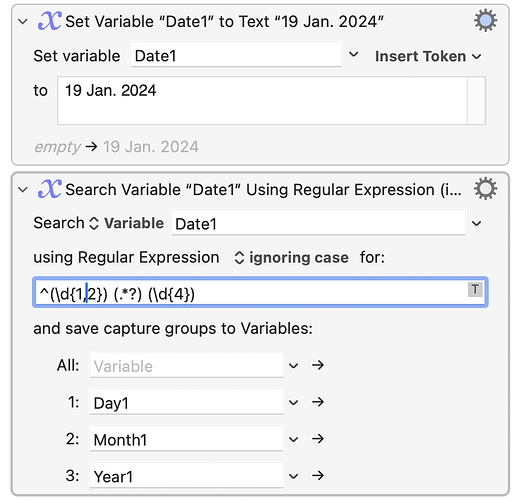
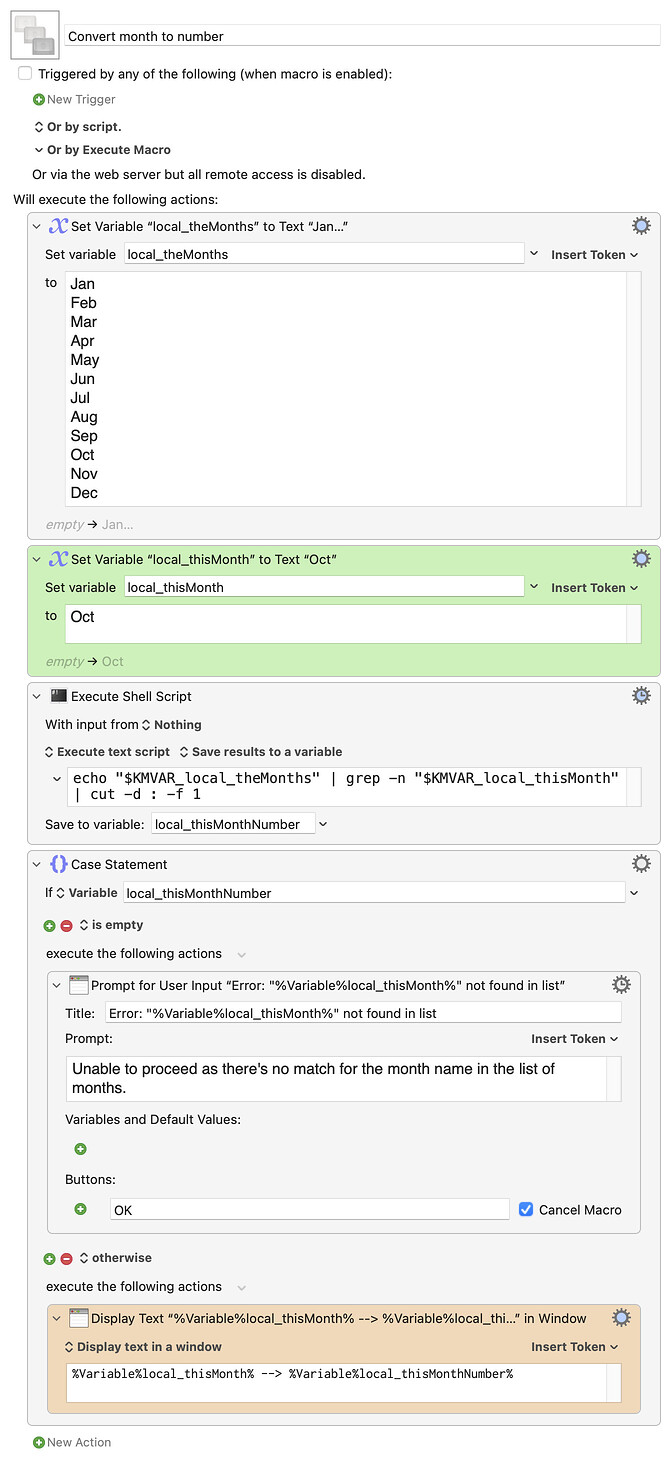
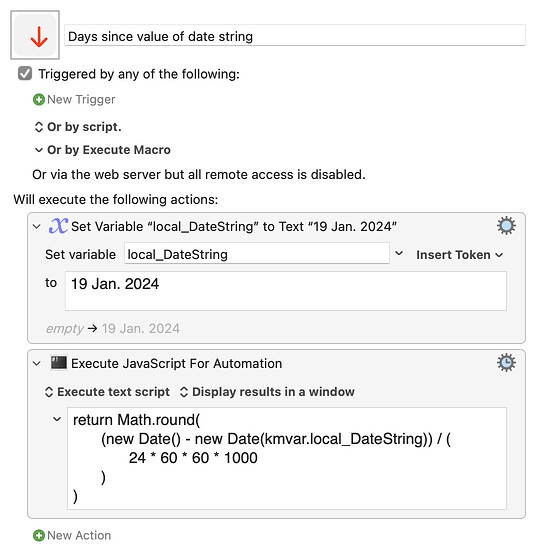
I'm not surprised that nobody wanted to consider my mathematical solution to the problem "Convert JAN to 1, FEB to 2, etc." As I said, it was an academic problem.
Here's the overview of my solution anyway, for the record... My first idea was to consider if there was a mathematical way to add up the letters in the months' names to come up with the answer, like this:
J+A+N => 1
F+E+B => 2
etc.
In theory there might be variables named J,A,N,F,E,B that would satisfy the above equations. Since there are more variables than equations, there will be more than one solution. We need to find only one solution that solves all twelve equations for the 12 months of the year. There are 12 equtions, but there are fewer than 36 variables because many months used the same letters (e.g., J is used in JAN, JUN and JUL.) In fact there are so many duplicated letters that there are really only 19 variables with 12 equations. And we can reduced the number of variables and equations even further by some simple visual inspections. For example, these two equations:
J+U+N = 6
J+U+L = 7
...tell us that L=N+1. Finding additional ways to reduce the number of variables and equations is a fun exercise and I will leave it to the reader.
At this point I realized that the equations don't need to precisely EQUAL the numbers they need to turn into. That's because there are exactly 12 months and so if the letters in a month added up to 24 or 36 they would still mean "12" because we can use modulus arithmetic instead of equality. I'm not sure if this step is necessary to solve the puzzle, but it seemed to help me.
I actually wrote a simple program in KM to solve all possible values for J,A,N,F,E,B,... so that they added up to the number of the month. However it looked like that program would have taken one year to complete, so I decided to cheat a little. I plugged the reduced set of 8 formulas that I had into the math website called Wolfram Alpha and it came up with a set of solutions instantly. It's a good thing that I reduced the number of formulas from 12 to 8, because when I tried it again with all 12 formulas Wolfram Alpha said that my question was "too long."
Finally, I will show you the actual string I plugged into Wolfram Alpha to solve this problem:
solve J+A+11=0 (MOD 12);M+A+R=2 (MOD 12);F+E+B=1 (MOD 12);A+A+5+G=7 (MOD 12);S+E+M+1=8 (MOD 12);O+C+T=9 (MOD 12);11+O+V=10 (MOD 12);D+E+C=11 (MOD 12)
This gave me this:
E = -C - D + 11 and F = -B + C + D - 10 and G = 2 - 2 A and J = -A - 11 and R = -A - M + 2 and S = C + D - M - 4 and T = -C - O + 9 and V = -O - 1
...which I was able to use to create my one line result, which was this...
sed "s/ /;((0/" | tr ' ' ';' | sed "s/[ABCDLMO]//g;s/E/+11/;s/F/+2/;s/G/+2/;s/J/+1/;s/N/+11/;s/P/+1/;s/R/+2/;s/S/+8/;s/T/+9/;s/U/+5/;s/V/+11/;s/Y/4/;s/./)%12)+1/" | bc | tr '\n' ' '