How to type progressional numbers?

Questions & Suggestions
1

I want to create a macro that types 001, 002, 003 … all the way to 999. How do I do that?

2

Here's one way:

Type Progressional Numbers.kmmacros (3.4 KB)
44 PM

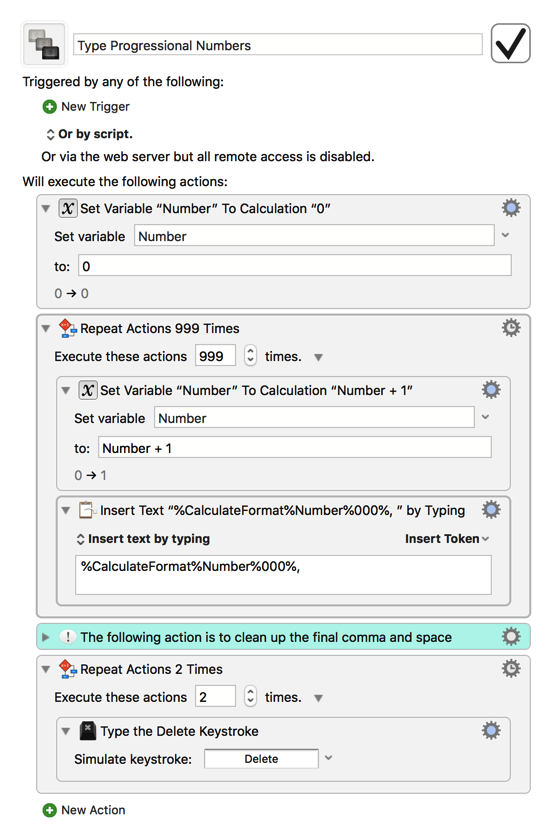
The key to typing the numbers with three digits is the %CalculateFormat% token, which you can read more about here: https://wiki.keyboardmaestro.com/token/CalculateFormat

3

For some reason when I type Number + 1 the + 1 is in red and it says empty -> instead of 0 -> 1

4

Also when I set Number to Calculation 0 it says empty -> 0

5

The reason it says “empty” is because the Number variable doesn’t yet exist on your system. The value after the → shows what the variable’s value will be once that action is executed. Try running the macro once (you may want to set it to 5 or 10 instead of 999 the first time to ensure it works) and from then on, it will show up like it does in my screenshot.

6

Hey @Patrick_Ma,

Do you really need to type the numbers out?

Or can you just paste the sequence?

If the latter is acceptable then something like this will work nicely.

-Chris

Insert Numerical Sequence.kmmacros (4.8 KB)

1 Like
7

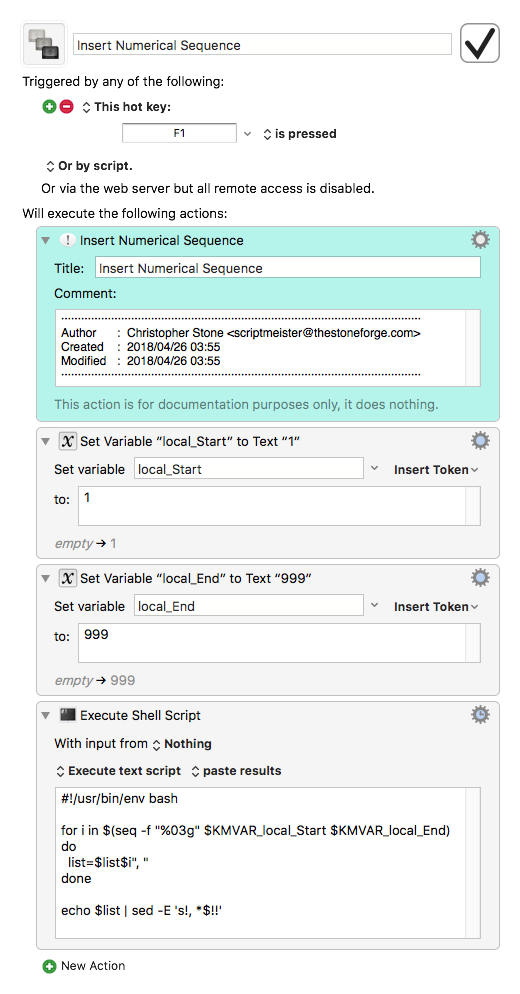
Or, in a Javascript action

const main = () =>
    enumFromToInt(1, 999)
    .map(x => justifyRight(3, '0', x.toString()))
    .join('\n');

In full:

(() => {
    'use strict';

    const main = () =>
        enumFromToInt(1, 999)
        .map(x => justifyRight(3, '0', x.toString()))
        .join('\n');



    // GENERIC FUNCTIONS --------------------------------------

    // enumFromToInt :: Int -> Int -> [Int]
    const enumFromToInt = (m, n) =>
        Array.from({
            length: 1 + (n - m)
        }, (_, i) => m + i)

    // justifyRight :: Int -> Char -> String -> String
    const justifyRight = (n, cFiller, strText) =>
        n > strText.length ? (
            (cFiller.repeat(n) + strText)
            .slice(-n)
        ) : strText;

    // MAIN ---------------------------------------------------
    return main();
})();
1 Like
8

Or, generalising a little in a more classical (if less actively maintained) language:

-- zeroPaddedIntegerSeries :: Int -> Int -> String
on zeroPaddedIntegerSeries(intFrom, intTo)
    script padded
        property w : length of (intTo as string)
        on |λ|(n)
            justifyRight(w, "0", n as string)
        end |λ|
    end script
    
    unlines(map(padded, enumFromToInt(intFrom, intTo)))
end zeroPaddedIntegerSeries

-- TEST -----------------------------------------------------
on run
    
    zeroPaddedIntegerSeries(1, 999)
    
end run


-- GENERIC FUNCTIONS ------------------------------------------------------------------

-- enumFromToInt :: Int -> Int -> [Int]
on enumFromToInt(m, n)
    if m ≤ n then
        set lst to {}
        repeat with i from m to n
            set end of lst to i
        end repeat
        return lst
    else
        return {}
    end if
end enumFromToInt

-- justifyRight :: Int -> Char -> String -> String
on justifyRight(n, cFiller, strText)
    if n > length of strText then
        text -n thru -1 of ((replicate(n, cFiller) as text) & strText)
    else
        strText
    end if
end justifyRight

-- map :: (a -> b) -> [a] -> [b]
on map(f, xs)
    tell mReturn(f)
        set lng to length of xs
        set lst to {}
        repeat with i from 1 to lng
            set end of lst to |λ|(item i of xs, i, xs)
        end repeat
        return lst
    end tell
end map

-- Lift 2nd class handler function into 1st class script wrapper
-- mReturn :: First-class m => (a -> b) -> m (a -> b)
on mReturn(f)
    if class of f is script then
        f
    else
        script
            property |λ| : f
        end script
    end if
end mReturn

-- Egyptian multiplication - progressively doubling a list, appending
-- stages of doubling to an accumulator where needed for binary 
-- assembly of a target length
-- replicate :: Int -> a -> [a]
on replicate(n, a)
    set out to {}
    if n < 1 then return out
    set dbl to {a}
    
    repeat while (n > 1)
        if (n mod 2) > 0 then set out to out & dbl
        set n to (n div 2)
        set dbl to (dbl & dbl)
    end repeat
    return out & dbl
end replicate

-- unlines :: [String] -> String
on unlines(xs)
    set {dlm, my text item delimiters} to ¬
        {my text item delimiters, linefeed}
    set str to xs as text
    set my text item delimiters to dlm
    str
end unlines
9

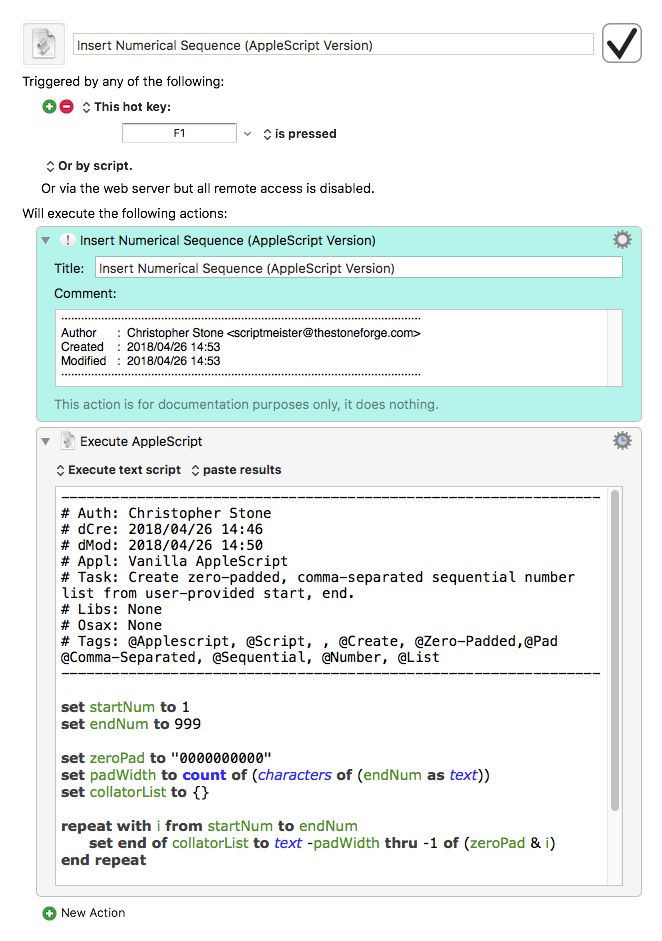
A straightforward vanilla AppleScript method.

-Chris

Insert Numerical Sequence (AppleScript Version).kmmacros (5.3 KB)

1 Like
10

@ccstone @ComplexPoint Y’all crack me up with your dueling solutions :slightly_smiling_face:

3 Likes
11

All of these approaches are optimised for difference purposes :slight_smile:

I can absolutely understand how Chris sees straightforwardness and brevity in composing a sequence of actions, and he can probably see why I might prefer to compose a nest of reusable functions, and create another one.

At the same time, on the notion of ‘straightforwardness’ we may also notice that:

  • both versions require only about 9-10 lines of new code,
  • one of them involves a single state transition in the global namespace, leaving behind only (reusable) function name-bindings, while the other involves 1004 state changes in the global name-space, leaving behind six (non-function) bound names.

One is likely to run a little faster, though the difference may be subliminal, while the the other is possibly a bit faster to write, though the difference is probably only a minute or two.

It just depends on what you happen to need at a given moment : -)

2 Likes