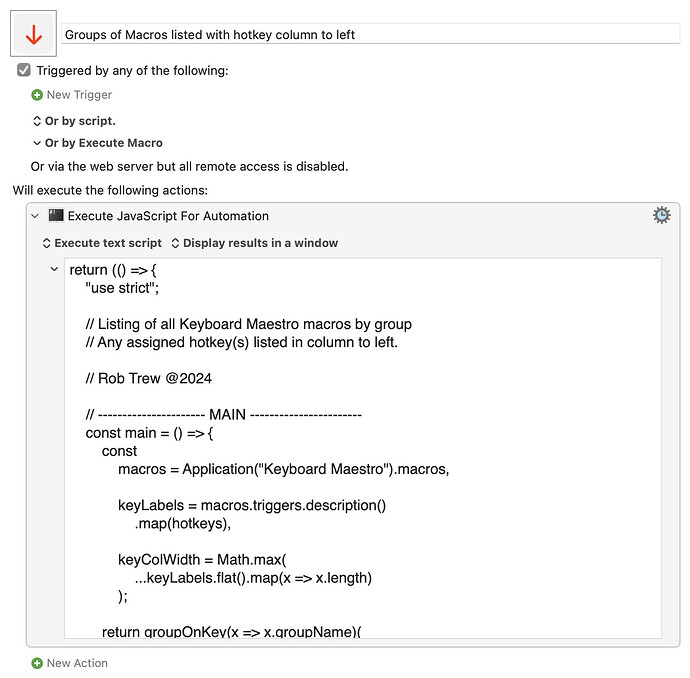
A variant on this theme which lists macros:
- by group,
- with assigned hotkeys in a left-hand column.
Groups of Macros listed with hotkey column to left.kmmacros (8.6 KB)
Expand disclosure triangle to view JS source
(() => {
"use strict";
// Listing of all Keyboard Maestro macros by group
// Any assigned hotkey(s) listed in column to left.
// Rob Trew @2024
// ---------------------- MAIN -----------------------
const main = () => {
const
macros = Application("Keyboard Maestro").macros,
keyLabels = macros.triggers.description()
.map(hotkeys),
keyColWidth = Math.max(
...keyLabels.flat().map(x => x.length)
);
return groupOnKey(x => x.groupName)(
sortOn(x => x.groupName)(
zipWithN(
groupName => macroName => triggers => ({
groupName, macroName, triggers
}),
macros.macroGroup.name(),
macros.name(),
keyLabels
)
)
)
.map(groupListing(keyColWidth))
.join("\n")
};
// --------------- MACRO GROUP LISTING ---------------
// groupListing :: Int -> (String, [Macro]) -> String
const groupListing = keyColWidth =>
([groupName, macros]) => [
`\n${toUpper(groupName)}`,
...macros.flatMap(macro => {
const
hs = macro.triggers,
n = hs.length,
xs = zipWithLong(
k => name =>
`${k.padEnd(keyColWidth)}\t${name}`
)(
hs
)([
macro.macroName
]);
return 0 < n
? indentedText(xs)
: `\t${" ".repeat(keyColWidth)}${indentedText(xs)}`;
})
]
.join("\n");
// hotkeys :: [String] -> [String]
const hotkeys = xs =>
xs.flatMap(
k => k.startsWith("The Hot Key")
? [keyPart(k)]
: []
);
// keyPart :: String -> String
const keyPart = s =>
s.slice(12, -11);
// indentedText :: [String] -> String
const indentedText = xs =>
xs.map(x => `\t${x}`)
.join("\n");
// --------------------- GENERIC ---------------------
// comparing :: Ord a => (b -> a) -> b -> b -> Ordering
const comparing = f =>
// The ordering of f(x) and f(y) as a value
// drawn from {-1, 0, 1}, representing {LT, EQ, GT}.
x => y => {
const
a = f(x),
b = f(y);
return a < b
? -1
: a > b
? 1
: 0;
};
// groupBy :: (a -> a -> Bool) -> [a] -> [[a]]
const groupBy = eqOp =>
// A list of lists, each containing only elements
// equal under the given equality operator, such
// that the concatenation of these lists is xs.
xs => 0 < xs.length
? (() => {
const [h, ...t] = xs;
const [groups, g] = t.reduce(
([gs, a], x) => eqOp(a[0])(x)
? [gs, [...a, x]]
: [[...gs, a], [x]],
[[], [h]]
);
return [...groups, g];
})()
: [];
// groupOnKey :: Eq k => (a -> k) -> [a] -> [(k, [a])]
const groupOnKey = f =>
// A list of (k, [a]) tuples, in which each [a]
// contains only elements for which f returns the
// same value, and in which k is that value.
// The concatenation of the [a] in each tuple === xs.
xs => 0 < xs.length
? groupBy(a => b => a[0] === b[0])(
xs.map(x => [f(x), x])
)
.map(gp => [
gp[0][0],
gp.map(ab => ab[1])
])
: [];
// maximumBy :: (a -> a -> Ordering) -> [a] -> a
const maximumBy = f =>
xs => 0 < xs.length
? xs.slice(1).reduce(
(a, x) => 0 < f(x)(a)
? x
: a,
xs[0]
)
: undefined;
// length :: [a] -> Int
const length = xs =>
// Returns Infinity over objects without finite
// length. This enables zip and zipWith to choose
// the shorter argument when one is non-finite,
// like cycle, repeat etc
"Node" !== xs.type
? "GeneratorFunction" !== (
xs.constructor.constructor.name
)
? xs.length
: Infinity
: lengthTree(xs);
// sortBy :: (a -> a -> Ordering) -> [a] -> [a]
const sortBy = f =>
// A copy of xs sorted by the comparator function f.
xs => xs.slice()
.sort((a, b) => f(a)(b));
// sortOn :: Ord b => (a -> b) -> [a] -> [a]
const sortOn = f =>
// Equivalent to sortBy(comparing(f)), but with f(x)
// evaluated only once for each x in xs.
// ('Schwartzian' decorate-sort-undecorate).
xs => sortBy(
comparing(x => x[0])
)(
xs.map(x => [f(x), x])
)
.map(x => x[1]);
// toUpper :: String -> String
const toUpper = s =>
s.toLocaleUpperCase();
// zipWithLong :: (a -> a -> a) -> [a] -> [a] -> [a]
const zipWithLong = f => {
// A list with the length of the *longer* of
// xs and ys, defined by zipping with a
// custom function, rather than with the
// default tuple constructor.
// Any unpaired values, where list lengths differ,
// are simply appended.
const go = xs =>
ys => 0 < xs.length
? 0 < ys.length
? [f(xs[0])(ys[0])].concat(
go(
xs.slice(1)
)(
ys.slice(1)
)
)
: xs
: ys;
return go;
};
// zipWithN :: (a -> b -> ... -> c) -> ([a], [b] ...) -> [c]
const zipWithN = (...args) =>
// Uncurried function of which the first argument is a
// curried function, and all remaining arguments are lists.
1 < args.length
? (
([f, ...xs]) => xs.slice(1).reduce(
// apZip
(gs, vs) => gs.map((g, i) => g(vs[i])),
xs[0].map(f)
)
)(args)
: [];
// MAIN ---
return main();
})();