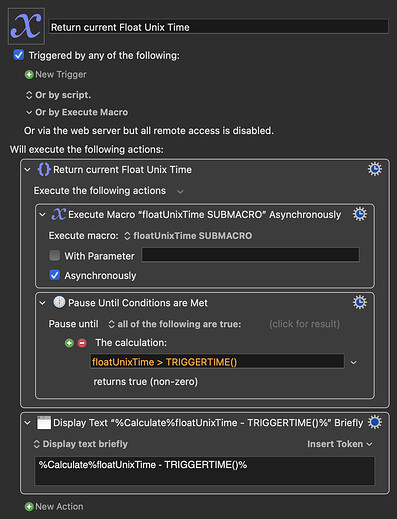
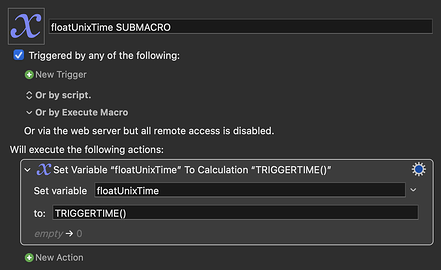
I have come to realised that I have thought completely wrong about the this whole topic of floating-point. And that the ideas I've had about a "float unix time" function does not make any sense.
I read somewhere that the decimal places of the TRIGGERTIME() is represented as "floating-point", reading that I thought about float in this context as an alternative number format, something it is; but I thought of this as if all of these decimals (often 8 of them) as something that could be translated to "fixed-point" numbers with some level of unambiguous precision — something I have come to understand it isn't. It is probably this fact that you all here have tried to explain to me, but I am slow in understanding these things.
Below is an explanation of how I now understand the floating-point represented decimal places given by the TRIGGERTIME()-function, but please du chime in with corrections and further elaboration on the subject, as I really do want to learn more about this.
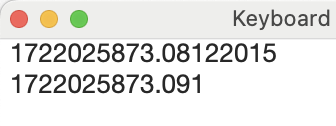
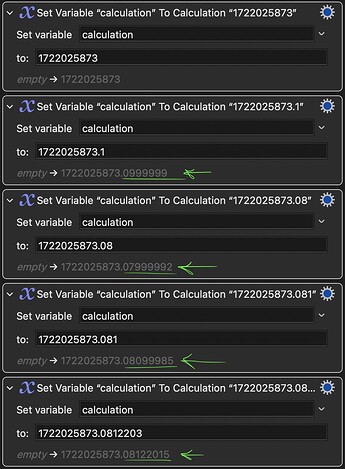
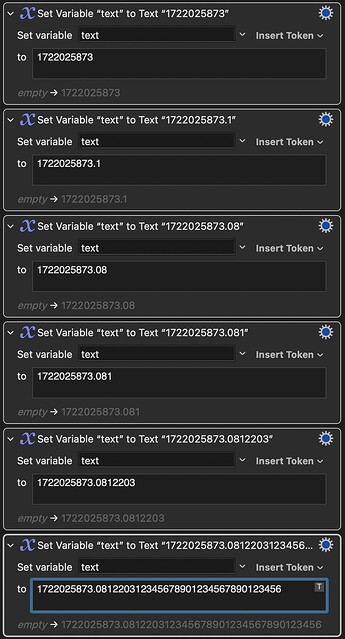
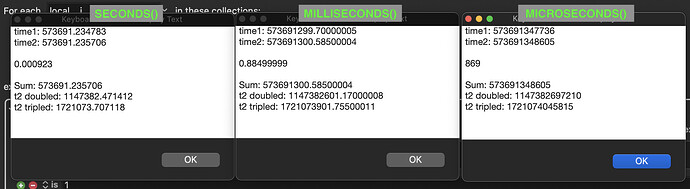
Beware that these floating point glitches can already show up in calculations on numbers of the 10-digit number with 3 decimal places, as with Unix Time with Milliseconds, as can be seen here:
One workaround for performing calculations on Unix Time with millisecond precision is to perform the calculations on the number as an integer number of millisecond, as non of the 13-digit numbers in this range seems to suffer of lost precision.
Calculated numbers from 1722025873000 to 1722025873999 with full precision
1722025873000,1722025873001,1722025873002,1722025873003,1722025873004,1722025873005,1722025873006,1722025873007,1722025873008,1722025873009,1722025873010,1722025873011,1722025873012,1722025873013,1722025873014,1722025873015,1722025873016,1722025873017,1722025873018,1722025873019,1722025873020,1722025873021,1722025873022,1722025873023,1722025873024,1722025873025,1722025873026,1722025873027,1722025873028,1722025873029,1722025873030,1722025873031,1722025873032,1722025873033,1722025873034,1722025873035,1722025873036,1722025873037,1722025873038,1722025873039,1722025873040,1722025873041,1722025873042,1722025873043,1722025873044,1722025873045,1722025873046,1722025873047,1722025873048,1722025873049,1722025873050,1722025873051,1722025873052,1722025873053,1722025873054,1722025873055,1722025873056,1722025873057,1722025873058,1722025873059,1722025873060,1722025873061,1722025873062,1722025873063,1722025873064,1722025873065,1722025873066,1722025873067,1722025873068,1722025873069,1722025873070,1722025873071,1722025873072,1722025873073,1722025873074,1722025873075,1722025873076,1722025873077,1722025873078,1722025873079,1722025873080,1722025873081,1722025873082,1722025873083,1722025873084,1722025873085,1722025873086,1722025873087,1722025873088,1722025873089,1722025873090,1722025873091,1722025873092,1722025873093,1722025873094,1722025873095,1722025873096,1722025873097,1722025873098,1722025873099,1722025873100,1722025873101,1722025873102,1722025873103,1722025873104,1722025873105,1722025873106,1722025873107,1722025873108,1722025873109,1722025873110,1722025873111,1722025873112,1722025873113,1722025873114,1722025873115,1722025873116,1722025873117,1722025873118,1722025873119,1722025873120,1722025873121,1722025873122,1722025873123,1722025873124,1722025873125,1722025873126,1722025873127,1722025873128,1722025873129,1722025873130,1722025873131,1722025873132,1722025873133,1722025873134,1722025873135,1722025873136,1722025873137,1722025873138,1722025873139,1722025873140,1722025873141,1722025873142,1722025873143,1722025873144,1722025873145,1722025873146,1722025873147,1722025873148,1722025873149,1722025873150,1722025873151,1722025873152,1722025873153,1722025873154,1722025873155,1722025873156,1722025873157,1722025873158,1722025873159,1722025873160,1722025873161,1722025873162,1722025873163,1722025873164,1722025873165,1722025873166,1722025873167,1722025873168,1722025873169,1722025873170,1722025873171,1722025873172,1722025873173,1722025873174,1722025873175,1722025873176,1722025873177,1722025873178,1722025873179,1722025873180,1722025873181,1722025873182,1722025873183,1722025873184,1722025873185,1722025873186,1722025873187,1722025873188,1722025873189,1722025873190,1722025873191,1722025873192,1722025873193,1722025873194,1722025873195,1722025873196,1722025873197,1722025873198,1722025873199,1722025873200,1722025873201,1722025873202,1722025873203,1722025873204,1722025873205,1722025873206,1722025873207,1722025873208,1722025873209,1722025873210,1722025873211,1722025873212,1722025873213,1722025873214,1722025873215,1722025873216,1722025873217,1722025873218,1722025873219,1722025873220,1722025873221,1722025873222,1722025873223,1722025873224,1722025873225,1722025873226,1722025873227,1722025873228,1722025873229,1722025873230,1722025873231,1722025873232,1722025873233,1722025873234,1722025873235,1722025873236,1722025873237,1722025873238,1722025873239,1722025873240,1722025873241,1722025873242,1722025873243,1722025873244,1722025873245,1722025873246,1722025873247,1722025873248,1722025873249,1722025873250,1722025873251,1722025873252,1722025873253,1722025873254,1722025873255,1722025873256,1722025873257,1722025873258,1722025873259,1722025873260,1722025873261,1722025873262,1722025873263,1722025873264,1722025873265,1722025873266,1722025873267,1722025873268,1722025873269,1722025873270,1722025873271,1722025873272,1722025873273,1722025873274,1722025873275,1722025873276,1722025873277,1722025873278,1722025873279,1722025873280,1722025873281,1722025873282,1722025873283,1722025873284,1722025873285,1722025873286,1722025873287,1722025873288,1722025873289,1722025873290,1722025873291,1722025873292,1722025873293,1722025873294,1722025873295,1722025873296,1722025873297,1722025873298,1722025873299,1722025873300,1722025873301,1722025873302,1722025873303,1722025873304,1722025873305,1722025873306,1722025873307,1722025873308,1722025873309,1722025873310,1722025873311,1722025873312,1722025873313,1722025873314,1722025873315,1722025873316,1722025873317,1722025873318,1722025873319,1722025873320,1722025873321,1722025873322,1722025873323,1722025873324,1722025873325,1722025873326,1722025873327,1722025873328,1722025873329,1722025873330,1722025873331,1722025873332,1722025873333,1722025873334,1722025873335,1722025873336,1722025873337,1722025873338,1722025873339,1722025873340,1722025873341,1722025873342,1722025873343,1722025873344,1722025873345,1722025873346,1722025873347,1722025873348,1722025873349,1722025873350,1722025873351,1722025873352,1722025873353,1722025873354,1722025873355,1722025873356,1722025873357,1722025873358,1722025873359,1722025873360,1722025873361,1722025873362,1722025873363,1722025873364,1722025873365,1722025873366,1722025873367,1722025873368,1722025873369,1722025873370,1722025873371,1722025873372,1722025873373,1722025873374,1722025873375,1722025873376,1722025873377,1722025873378,1722025873379,1722025873380,1722025873381,1722025873382,1722025873383,1722025873384,1722025873385,1722025873386,1722025873387,1722025873388,1722025873389,1722025873390,1722025873391,1722025873392,1722025873393,1722025873394,1722025873395,1722025873396,1722025873397,1722025873398,1722025873399,1722025873400,1722025873401,1722025873402,1722025873403,1722025873404,1722025873405,1722025873406,1722025873407,1722025873408,1722025873409,1722025873410,1722025873411,1722025873412,1722025873413,1722025873414,1722025873415,1722025873416,1722025873417,1722025873418,1722025873419,1722025873420,1722025873421,1722025873422,1722025873423,1722025873424,1722025873425,1722025873426,1722025873427,1722025873428,1722025873429,1722025873430,1722025873431,1722025873432,1722025873433,1722025873434,1722025873435,1722025873436,1722025873437,1722025873438,1722025873439,1722025873440,1722025873441,1722025873442,1722025873443,1722025873444,1722025873445,1722025873446,1722025873447,1722025873448,1722025873449,1722025873450,1722025873451,1722025873452,1722025873453,1722025873454,1722025873455,1722025873456,1722025873457,1722025873458,1722025873459,1722025873460,1722025873461,1722025873462,1722025873463,1722025873464,1722025873465,1722025873466,1722025873467,1722025873468,1722025873469,1722025873470,1722025873471,1722025873472,1722025873473,1722025873474,1722025873475,1722025873476,1722025873477,1722025873478,1722025873479,1722025873480,1722025873481,1722025873482,1722025873483,1722025873484,1722025873485,1722025873486,1722025873487,1722025873488,1722025873489,1722025873490,1722025873491,1722025873492,1722025873493,1722025873494,1722025873495,1722025873496,1722025873497,1722025873498,1722025873499,1722025873500,1722025873501,1722025873502,1722025873503,1722025873504,1722025873505,1722025873506,1722025873507,1722025873508,1722025873509,1722025873510,1722025873511,1722025873512,1722025873513,1722025873514,1722025873515,1722025873516,1722025873517,1722025873518,1722025873519,1722025873520,1722025873521,1722025873522,1722025873523,1722025873524,1722025873525,1722025873526,1722025873527,1722025873528,1722025873529,1722025873530,1722025873531,1722025873532,1722025873533,1722025873534,1722025873535,1722025873536,1722025873537,1722025873538,1722025873539,1722025873540,1722025873541,1722025873542,1722025873543,1722025873544,1722025873545,1722025873546,1722025873547,1722025873548,1722025873549,1722025873550,1722025873551,1722025873552,1722025873553,1722025873554,1722025873555,1722025873556,1722025873557,1722025873558,1722025873559,1722025873560,1722025873561,1722025873562,1722025873563,1722025873564,1722025873565,1722025873566,1722025873567,1722025873568,1722025873569,1722025873570,1722025873571,1722025873572,1722025873573,1722025873574,1722025873575,1722025873576,1722025873577,1722025873578,1722025873579,1722025873580,1722025873581,1722025873582,1722025873583,1722025873584,1722025873585,1722025873586,1722025873587,1722025873588,1722025873589,1722025873590,1722025873591,1722025873592,1722025873593,1722025873594,1722025873595,1722025873596,1722025873597,1722025873598,1722025873599,1722025873600,1722025873601,1722025873602,1722025873603,1722025873604,1722025873605,1722025873606,1722025873607,1722025873608,1722025873609,1722025873610,1722025873611,1722025873612,1722025873613,1722025873614,1722025873615,1722025873616,1722025873617,1722025873618,1722025873619,1722025873620,1722025873621,1722025873622,1722025873623,1722025873624,1722025873625,1722025873626,1722025873627,1722025873628,1722025873629,1722025873630,1722025873631,1722025873632,1722025873633,1722025873634,1722025873635,1722025873636,1722025873637,1722025873638,1722025873639,1722025873640,1722025873641,1722025873642,1722025873643,1722025873644,1722025873645,1722025873646,1722025873647,1722025873648,1722025873649,1722025873650,1722025873651,1722025873652,1722025873653,1722025873654,1722025873655,1722025873656,1722025873657,1722025873658,1722025873659,1722025873660,1722025873661,1722025873662,1722025873663,1722025873664,1722025873665,1722025873666,1722025873667,1722025873668,1722025873669,1722025873670,1722025873671,1722025873672,1722025873673,1722025873674,1722025873675,1722025873676,1722025873677,1722025873678,1722025873679,1722025873680,1722025873681,1722025873682,1722025873683,1722025873684,1722025873685,1722025873686,1722025873687,1722025873688,1722025873689,1722025873690,1722025873691,1722025873692,1722025873693,1722025873694,1722025873695,1722025873696,1722025873697,1722025873698,1722025873699,1722025873700,1722025873701,1722025873702,1722025873703,1722025873704,1722025873705,1722025873706,1722025873707,1722025873708,1722025873709,1722025873710,1722025873711,1722025873712,1722025873713,1722025873714,1722025873715,1722025873716,1722025873717,1722025873718,1722025873719,1722025873720,1722025873721,1722025873722,1722025873723,1722025873724,1722025873725,1722025873726,1722025873727,1722025873728,1722025873729,1722025873730,1722025873731,1722025873732,1722025873733,1722025873734,1722025873735,1722025873736,1722025873737,1722025873738,1722025873739,1722025873740,1722025873741,1722025873742,1722025873743,1722025873744,1722025873745,1722025873746,1722025873747,1722025873748,1722025873749,1722025873750,1722025873751,1722025873752,1722025873753,1722025873754,1722025873755,1722025873756,1722025873757,1722025873758,1722025873759,1722025873760,1722025873761,1722025873762,1722025873763,1722025873764,1722025873765,1722025873766,1722025873767,1722025873768,1722025873769,1722025873770,1722025873771,1722025873772,1722025873773,1722025873774,1722025873775,1722025873776,1722025873777,1722025873778,1722025873779,1722025873780,1722025873781,1722025873782,1722025873783,1722025873784,1722025873785,1722025873786,1722025873787,1722025873788,1722025873789,1722025873790,1722025873791,1722025873792,1722025873793,1722025873794,1722025873795,1722025873796,1722025873797,1722025873798,1722025873799,1722025873800,1722025873801,1722025873802,1722025873803,1722025873804,1722025873805,1722025873806,1722025873807,1722025873808,1722025873809,1722025873810,1722025873811,1722025873812,1722025873813,1722025873814,1722025873815,1722025873816,1722025873817,1722025873818,1722025873819,1722025873820,1722025873821,1722025873822,1722025873823,1722025873824,1722025873825,1722025873826,1722025873827,1722025873828,1722025873829,1722025873830,1722025873831,1722025873832,1722025873833,1722025873834,1722025873835,1722025873836,1722025873837,1722025873838,1722025873839,1722025873840,1722025873841,1722025873842,1722025873843,1722025873844,1722025873845,1722025873846,1722025873847,1722025873848,1722025873849,1722025873850,1722025873851,1722025873852,1722025873853,1722025873854,1722025873855,1722025873856,1722025873857,1722025873858,1722025873859,1722025873860,1722025873861,1722025873862,1722025873863,1722025873864,1722025873865,1722025873866,1722025873867,1722025873868,1722025873869,1722025873870,1722025873871,1722025873872,1722025873873,1722025873874,1722025873875,1722025873876,1722025873877,1722025873878,1722025873879,1722025873880,1722025873881,1722025873882,1722025873883,1722025873884,1722025873885,1722025873886,1722025873887,1722025873888,1722025873889,1722025873890,1722025873891,1722025873892,1722025873893,1722025873894,1722025873895,1722025873896,1722025873897,1722025873898,1722025873899,1722025873900,1722025873901,1722025873902,1722025873903,1722025873904,1722025873905,1722025873906,1722025873907,1722025873908,1722025873909,1722025873910,1722025873911,1722025873912,1722025873913,1722025873914,1722025873915,1722025873916,1722025873917,1722025873918,1722025873919,1722025873920,1722025873921,1722025873922,1722025873923,1722025873924,1722025873925,1722025873926,1722025873927,1722025873928,1722025873929,1722025873930,1722025873931,1722025873932,1722025873933,1722025873934,1722025873935,1722025873936,1722025873937,1722025873938,1722025873939,1722025873940,1722025873941,1722025873942,1722025873943,1722025873944,1722025873945,1722025873946,1722025873947,1722025873948,1722025873949,1722025873950,1722025873951,1722025873952,1722025873953,1722025873954,1722025873955,1722025873956,1722025873957,1722025873958,1722025873959,1722025873960,1722025873961,1722025873962,1722025873963,1722025873964,1722025873965,1722025873966,1722025873967,1722025873968,1722025873969,1722025873970,1722025873971,1722025873972,1722025873973,1722025873974,1722025873975,1722025873976,1722025873977,1722025873978,1722025873979,1722025873980,1722025873981,1722025873982,1722025873983,1722025873984,1722025873985,1722025873986,1722025873987,1722025873988,1722025873989,1722025873990,1722025873991,1722025873992,1722025873993,1722025873994,1722025873995,1722025873996,1722025873997,1722025873998,1722025873999,
But the fp-glitching does not really seem to affekt the precision of these numbers to any significant degree, milliseconds precision, and even beyond, seem to hold with with numbers in this range, so I believe one can "safely" perform arithmetic on these "glitched" numbers, but I have not yet explored this enough for any level of certainty, so do chime in if this is something that could lead to undesirable results