I there a way I can see how long it will take for the macro to run?
would like to have a little bit of an idea on how long it will take to run a macro I have. I could add up all of the wait times and the multiply that by the number of times the action will repeat but I am hoping that there is something that gives an "estimated time saved" or something like that! Like a word count feature. Time it will take to run a macro
You have stumbled upon a phenomenon known as the Halting Problem, which focuses on whether a program will ever finish, but includes the more specific question of "how long will the program take to finish?"
It is mathematically proven that this problem is undecidable. That does not mean it can't be solved for specific cases, but it cannot be solved in the general case. There are many specific cases that are easy to solve, such as if your macro has no actions. But you want the value to be calculated with conditions and loops, which is exponentially more difficult.
BUT DON'T LOSE HOPE!...
It is fairly easy to measure how long a macro has taken. For example, you could assign the current time to a clock variable at the start of the macro, then when the macro ends, subtract that from the current clock, and either display or save the variable. What I would do is not just save the variable, but save all the duration values in a variable list or a dictionary. Then I could display all the durations later. In fact, that's such a great idea, I think I'm going to work on that today.
I've just written a macro template that lets you record macro durations (every time the macro runs) and lets you report on the average macro duration (and even the standard deviation.) It also lets you clear the history. If you want your macros to record and report their durations, you can use this template.
I wrote a fairly detailed time tracker that lets you run a bunch of sub-times during the macro run, so you can see how long each section takes:
-rob.
Cool. Thanks. Sorry if I stepped on your turf here. But I enjoy rewriting my own macros, and my approach may differ from yours and might be useful too. For example I use dictionaries, and I make an attempt to fix the midnight bug when using the SECONDS() function.
No toe stepping, just providing another alternative. I think mine should work fine across midnight, though I admit I never tested it, as it simply records the start time and stop time since the epoch.
The main reason I wrote mine was I wanted timings on sections of macros in an easy-to-get and easy-to-read fashion.
-rob.
Even though they are real numbers, all epoch times are rounded to the nearest second, did you know that? So if you are recording epoch times you are not getting fractional second resolution.
And the SECONDS() function is fractional, but is based on a midnight starting point. Therefore it will return erroneous times around midnight.
That's not what the wiki says about it:
"The SECONDS() function returns the time in fractional seconds since the Mac started."
Why would that be off at any time around midnight? It should be irrelevant.
EDIT: And I was wrong about my timer macro; it uses the SECONDS() token, not the epoch times. I'm genuinely curious why that might be wrong around midnight, though?
-rob.
The reason is that I'm a complete bozo who saw the number range from very small to very large and assumed that the reset was midnight, not a reboot. So I retract my claim that there could be a midnight bug. Hopefully I'm not banned from these forums, but if you want to give me a short ban, I'd accept it. A week seems fine.
But what I said about epoch times, I still stand by. I remain confident that epoch times look like the have high resolution, but because they are based on unix time, which is rounded to the nearest second, they can't return fractional numbers (of seconds), and therefore are of limited use for timing things, despite the fact that they return high precision real numbers. And you did say you used epoch times, so I was implying that there might be a bug in your code. However you have since re-stated that you are not using epoch times, but using SECONDS(), so that means you won't have a bug.
So for example, the wiki says this about JD():
A JulianDate (JD) is days (and fractions of days) since January 1, 4713 BC Greenwich noon.
And if you look at the results of JD(), you get a number like:
2460477.65442131
By looking at that, you can see 8 decimal places, so one might think that the precision of JD() is one hundred millionth of a day, which would be "24 times 60 times 60"/100000000=0.000864. But that's very misleading because the true resolution of JD() is 1.0 seconds, not 0.000864 seconds.
In my opinion, JD() should return no more than three decimal points of accuracy, or the wiki for JD() should state that only 3 decimal places have any meaning.
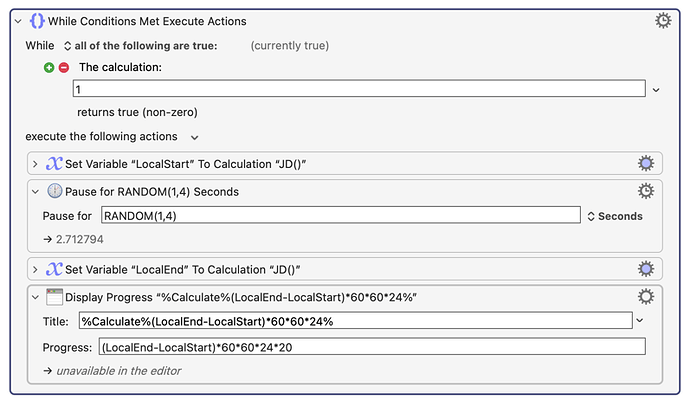
If you try this macro, you will realize that JD() does not resolve times to more than one second:
If you study the output, you will realize that JD() never gives 8 decimal places of accuracy, just three decimal places.
Sheez, no need for any of that! A public flogging will be more than sufficient! ![]()
![]()
![]()
Seriously, as I thought about it, I thought maybe there was something about the math KM did that made midnight troublesome, so that's why I went back and double-checked. Thanks for making me look—seriously!
I am far from an expert in Julian Dates, but I think (with a heavy emphasis on think) all those digits are required to get the one second accuracy when doing any sort of date calculations—and even then, that's not enough for true one-second accuracy.
Here's an example of two Julian Dates from running your macro, along with the difference between those dates, as well as the actual delay that the macro used (by saving the RAND() calculation to a var):
Start: 2460477.95769676
End: 2460477.95773148
Delta: 0.00003472
Actual: 3.64756101 seconds
The delta is the elapsed time of the macro as expressed as a portion of a Julian Date. To convert that elapsed time to seconds, given that it's stated as a portion of a full day, you need to multiply by the number of seconds in a day, which is 86,400:
0.00003472 * 86400 = 2.999808
So using Julian Dates for the time delta calculation, you would conclude that the elapsed time was three seconds, to a one-second accuracy. In reality, when rounded to the nearest second, the elapsed time was four seconds.
If Julian Dates only used three decimal places, though, you couldn't even calculate the seconds, as the numbers are identical to three places:
Start: 2460477.957
End: 2460477.957
Unless I'm not understanding something (which is very possible), that's why Julian Dates are shown to so many significant digits: It's not that the actual date is precise to that level of precision, but that that level of precision is needed to even extract the seconds when doing any time calculations.
I may be very wrong about this, though :).
-rob.